Ziele
Entsprechend dem design-basierten Ansatz werden die Ziele des Teilprojekts unter den Aspekten Design und Theorie betrachtet.
Design-Ebene
- Materialienkatalog zum Werkzeugeinsatz der blockbasierten Programmiersprache Scratch (https://scratch.mit.edu/) im Mathematikunterricht der Mittelstufe
- Designprinzipien für das begleitende Programmieren im Mathematikunterricht mit Scratch
Theorie-Ebene
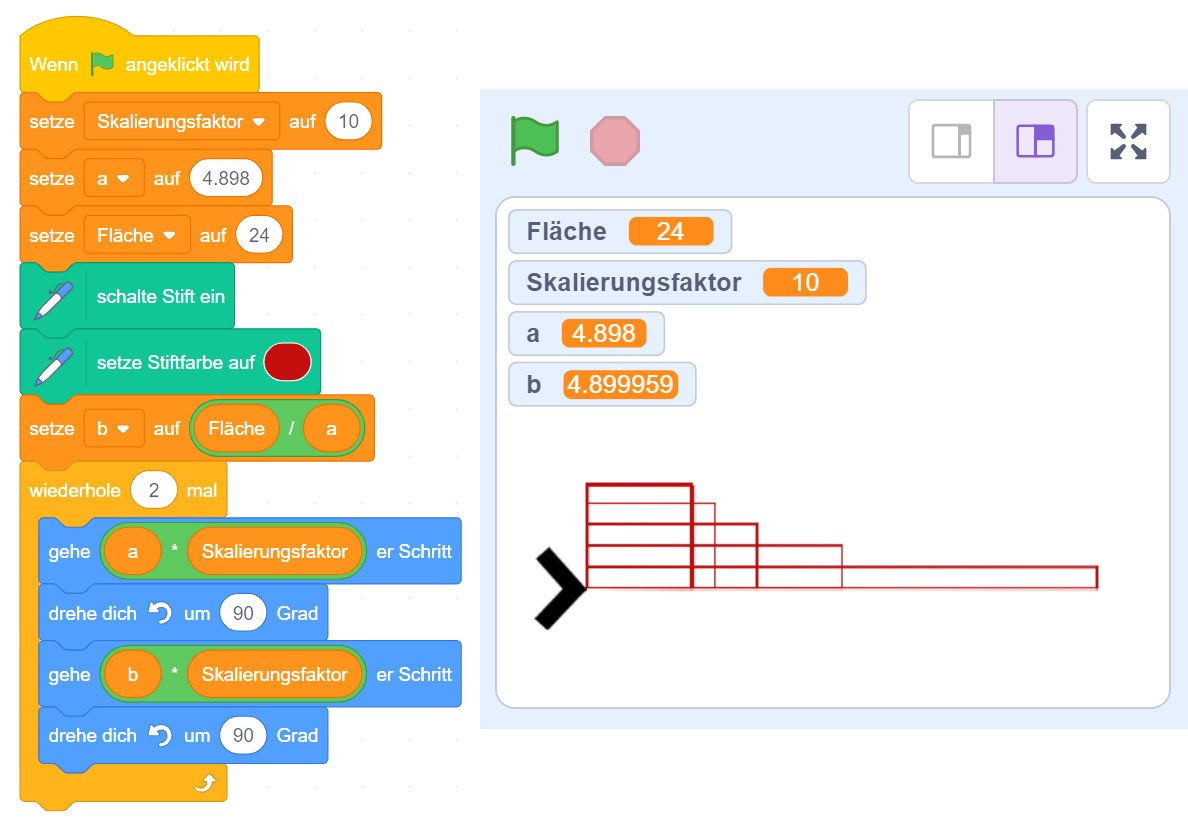
- Auftreten von CT-Aspekten und Praktiken beim Einsatz von Scratch im Mathematikunterricht
- Herausforderungen von Lehrkräften beim Einsatz von Scratch im Mathematikunterricht
- Einfluss von Programmieren auf Einstellungen zu Mathematik und MINT
Methodik
Das Projekt verfolgt einen design-basierten Ansatz. Entlang eines Schuljahres werden Materialien für den Mathematikunterricht einer 7. und 8. Klasse entwickelt, erprobt und evaluiert. Dabei werden zwei Makrozyklen (Eprobung der Materialien in zwei Schuljahren) durchlaufen, wobei innerhalb jedes Makrozyklus die Erprobung der Materialien die weitere Entwicklung beeinflusst. Die Auswertung der Materialien erfolgt primär durch qualitative Analyse von teilnehmenden Beobachtungen, unterstützt durch einzelne Fragebogenumfragen und verfolgt somit einen Mixed-Method-Ansatz.